Dynamic Heterogeneity in Amorphous Materials

Dynamical heterogeneity, spatiotemporal fluctuations in local dynamical behavior, may explain the statistical mechanics of amorphous solids that are mechanically rigid but have a disordered structure similar to that of a dense liquid.

From the point of view of statistical physics, glasses are mysterious materials. Glassy materials possess a mechanical rigidity, which is similar to that of a crystalline material. In a crystal, rigidity is a direct consequence of long-range periodic order: It is not possible to move a single particle in a perfect crystal (while preserving the crystalline order) without also moving an extensive set of neighbors [Fig. 1(a)]. While mechanically rigid—glasses do not seem to be characterized by any type of long-range order, see Fig. (b)—they resemble ordinary dense liquids. The comparison between crystals and glasses suggests that perhaps a more subtle symmetry breaking takes place during the formation of a glass, one that is not obvious to the naked eye. This conundrum has been a long-standing issue in condensed-matter physics

Figure 1: (a) A periodic crystalline structure does not flow because preserving the crystalline order requires moving an extensive set of particles. (b) A mechanically rigid glassy structure exhibits neither the long-range order of a crystal nor the large-scale density fluctuations observed at an ordinary critical point. (c) Large-scale critical density fluctuations near the critical point.


Experimentally, one faces the difficulty that liquids approaching the glass transition (with decreasing temperature, for example) become too viscous to flow on experimental timescales, and fall out of thermal equilibrium without any reproducible thermodynamic phase transition. It is tempting to interpret this dramatic dynamic slowing down as originating from an underlying phase transition or critical point. Near an ordinary critical point, large-scale spatial fluctuations develop, such as the density fluctuations in the example shown in Fig. 1(c), and the dynamics slows down [3]. However, no such fluctuations are detected near the glass transition [Fig. 1(b)]. Therefore, finding evidence of a phase transition underlying the physics of amorphous materials would represent important progress.

In the last decade, these questions have also come up in the field of soft condensed matter, in which disordered structures known as “jammed” materials [4] (foams, emulsions, colloidal gels, sandpiles) stop flowing when their density becomes large, without possessing long-range crystalline order, just like molecular glasses. J. D. Bernal [5] in the 1960s was one of the first physicists to suggest that disordered atomic fluids and granular packings could be investigated using similar tools and perhaps understood using similar theoretical concepts—an idea that has since remained highly popular [6].

Two decades of research on dynamic heterogeneity (described in the next section) in amorphous materials have established that the formation of rigid amorphous structures is indeed accompanied by nontrivial spatiotemporal fluctuations, which become stronger nearer the glassy phase and are characterized by growing dynamic correlation length scales [7]. In this article we revisit the mounting evidence—using mostly the example of supercooled liquids, where dynamic heterogeneity has been most widely analyzed—that the formation of amorphous materials is a complex collective phenomenon, which shares more similarities with ordinary critical points than the featureless structure shown in Fig. 1(b) would suggest.
What is dynamic heterogeneity?


The concept of dynamic heterogeneity as a key feature that characterizes disordered materials has slowly emerged from experimental studies of highly viscous molecular liquids approaching the glass transition. In these systems, relaxation spectra measured through mechanical or dielectric probes span a very broad range of relaxation times and are strongly nonexponential. This suggests the existence of wide distributions of relaxation rates.

What is the microscopic origin of these broad distributions? Looking again at the disordered structure in Fig. 1(b), it is natural to imagine that the presence of structural disorder implies that atoms in different environments move differently. The physical picture is that, at any given time, different regions in a liquid might relax in a different manner and at a different rate, thus producing broad distributions of relaxation times. However, when the system is close to the glass transition but not yet a glass, particles constantly move and rearrange, and so the distinction between different spatial environments can only hold over a finite duration.

Dynamic heterogeneity refers to the existence of transient spatial fluctuations in the local dynamical behavior. Dynamic heterogeneity is observed in virtually all disordered systems with glassy dynamics [7].

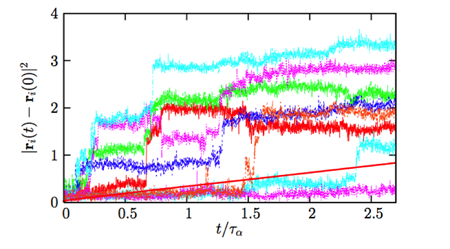
Direct confirmation of the heterogeneous character of the dynamics stems, for instance, from computer simulations of simple models of supercooled liquids (Fig. 2). Whereas the average displacement of a particle in a given time window of width t� is a smooth increasing function of t�, the time signals for individual particles shown in Fig. 2 have two important characteristics.

Figure 2: Time-resolved squared displacements of individual particles in a simple model of a glass-forming liquid. The average behavior is shown as the smooth full line. Individual trajectories are composed of long periods of time during which particles vibrate around well-defined positions, separated by rapid jumps that are widely distributed in time and occur at different times and frequencies for different particles.



(i) They are highly intermittent, composed of a succession of long periods of time where particles vibrate around well-defined locations that are separated by rapid “jumps.” The waiting times separating successive jumps are statistically broadly distributed.

(ii) The trajectories differ widely from one particle to another in the same system at the same time. Some particles undergo many jumps and move large distances while others are nearly immobile over the entire time window.

As with all other features related to dynamic heterogeneity, such observations cannot be made from ensemble-averaged measurements. Indeed, the characterization of dynamic heterogeneity requires the development of experimental techniques that are not only sensitive to average or typical behavior, but can also resolve the fluctuations. For theorists, the existence of dynamic heterogeneity implies that fluctuations need to be taken into account in the description of transport properties. Therefore, materials close to a glass transition differ qualitatively from ordinary fluids, where fluctuations can typically be neglected.

The intermittency of single-particle trajectories, while clearly indicating spatiotemporal fluctuations, does not tell us how these fluctuations are correlated in space. This point was first addressed in pioneering works with four-dimensional NMR [9] and direct probing of fluctuations at the nanoscopic scale using atomic force microscopy techniques in polymeric glasses [10]. Direct visualizations of molecular trajectories are not yet possible, but recent, very elegant experimental approaches using single-molecule spectroscopy are getting close to it [11,12]. Direct visualization is possible for different types of glasses, such as colloidal [13] and granular [14,15] assemblies. All these spatially resolved measurements indicate that extended regions of space transiently behave as fast and slow regions.
Need for high-order dynamic correlation functions


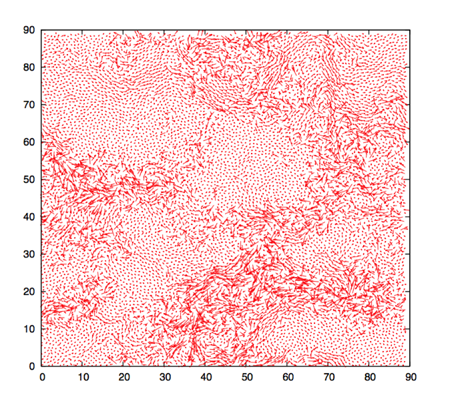
We have described dynamic heterogeneity as spatial variations in the local relaxation rate. Though hard to detect in an experiment, these fluctuations are observed in a computer simulation, where the position of each particle is known at each time step. In Fig. 3, we show an example of the visualization of spatially heterogeneous dynamics in a simple model of a supercooled liquid in two spatial dimensions. This visualization shows the existence of spatially extended “domains” where the amplitudes of single-particle displacements are correlated. These domains have no obvious counterpart in the density fluctuations [Fig. 1(b)] and only appear when dynamics is considered. However, the spatial fluctuations in Fig. 3 are reminiscent of the critical fluctuations in Fig. 1(c), with one major difference: while a thermodynamic quantity (the density) becomes critical in ordinary critical phenomena, fluctuations are only detected through dynamical quantities in highly viscous liquids.

Figure 3: Spatial map of single particle displacements in the simulation of a Lennard-Jones model of a supercooled liquid in two spartial dimensions. Arrows represent the displacement of each individual particle in a trajectory of duration comparable to the typical structural relaxation time. This map reveals that particles with different mobilities are spatially correlated.



To characterize the spatial fluctuations in Fig. 3 in a statistical manner, one must resolve the dynamics in both space and time and quantify deviations from the average behavior. To this end, one defines a “mobility,” ci(t,0)��(�,0), which quantifies how much particle i� moves between times t=0�=0 and t� (for instance ci(t)=exp[−|ri(t)−ri(0)|2/d2]��(�)=exp[-|r�(�)-r�(0)|2/�2], with d� of the order of the particle size). Given two particles at separation r�, one can measure the degree to which their mobilities are correlated. It is convenient to define a “mobility field” for a system composed of N� particles via

c(r;t,0)=∑Ni=1ci(t,0)δ[r−ri(0)],�(r;�,0)=∑�=1���(�,0)�[r-r�(0)],

(1)

where ri(t)r�(�) is the position of particle i� at time t�. The spatial correlations of the mobility are finally captured by the correlation function

G4(r;t)=⟨c(r;t,0)c(0;t,0)⟩−⟨c(r;t,0)⟩2,�4(�;�)=⟨�(r;�,0)�(0;�,0)⟩-⟨�(r;�,0)⟩2,

(2)

which depends only on the time t� and the distance r=|r|�=|r| as long as the ensemble average, denoted with brackets, is taken at equilibrium in a translationally invariant system; G4(r;t)�4(�;�) is known as a “four-point” dynamic correlation function as it measures correlations of motion between 00 and t� arising at two points, 00 and rr.

The analogy with fluctuations in critical systems becomes clear in Eq. (2) if one considers the mobility field c(r;t,0)�(r;�,0) as playing the role of the order parameter for the transition, characterized by nontrivial fluctuations and correlations near the glass transition. This analogy is now exploited in modern theoretical treatments [2].

The above definition of a real-space correlation function of the mobility represents a vital advance in the characterization of dynamical heterogeneity. For instance, it allows the language of field theory and critical phenomena to be used in studying dynamical fluctuations in glassy systems [16,17]. Like in critical phenomena, if one assumes the existence of a single dominant length scale ξ4�4, then one expects that for large distances the correlation function G4(r;t)�4(�;�) decays as

G4(r;t)≈A(t)[exp(−r/ξ4(t))]/rp,�4(�;�)≈�(�)[exp(-�/�4(�))]/��,

(3)

where p� is a critical exponent. It is also natural to define the susceptibility associated with the correlation function

χ4(t)=∫ddrG4(r;t).�4(�)=∫��r�4(�;�).

(4)

If the prefactor A(t)�(�) in Eq. (3) is known, the susceptibility χ4(t)�4(�) can be used to infer the typical number of particles involved in the correlated motion shown in Fig. 3. That is, χ4(t)�4(�) may be interpreted as the “volume” of the correlated clusters.

Further, χ4(t)�4(�) can also be obtained from the fluctuations of the total mobility C(t,0)=∫ddrc(r;t,0)�(�,0)=∫��r�(r;�,0), through

χ4(t)=N[⟨C(t,0)2⟩−⟨C(t,0)⟩2].�4(�)=�[⟨�(�,0)2⟩-⟨�(�,0)⟩2].

(5)

In practice, this formula permits an efficient measure of the degree of dynamical heterogeneity, at least in computer simulations and in those experiments where the dynamics can be spatially and temporally resolved. As long as c(r;t,0)�(r;�,0) appropriately quantifies atomic motion, χ4(t)�4(�) can be measured in a variety of systems, serving as a basis for comparing the extent of dynamical heterogeneity, and has become a central tool in characterizing dynamic heterogeneity in amorphous materials [7].
Four-point susceptibilities in molecular, colloidal, and granular glasses


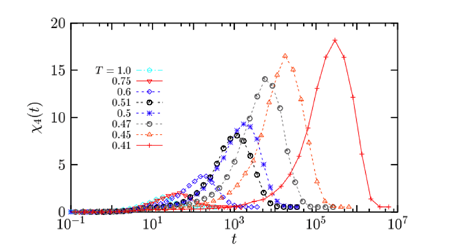
The dynamical function χ4(t)�4(�) has now been measured in computer simulations of many different glass-forming liquids, by molecular dynamics, Brownian, and Monte Carlo simulations [18–23]. An example is shown in Fig. 4 for a Lennard-Jones numerical model, but the qualitative behavior is similar in all cases [24–26]: as a function of time, χ4(t)�4(�) increases at first, it has a peak on a timescale of the order of the typical relaxation time of the fluid, and then it decreases at large times. This time dependence simply reflects the transient nature of the dynamical heterogeneity.

Figure 4: Time dependence of the susceptibility χ4(t)�4(�) that quantifies spontaneous fluctuations of the relaxation function in a molecular dynamics simulation of a supercooled liquid. For each temperature, χ4(t)�4(�) has a maximum, which shifts to larger times and has a larger value when T� is decreased, revealing the increasing length scale of dynamic heterogeneity in supercooled liquids that approach the glass transition.



The peak value of χ4(t)�4(�) approximately measures the volume over which structural relaxation processes are correlated. Therefore the most important result obtained from data such as those presented in Fig. 4 is the temperature evolution of the peak height, which is found to increase when the temperature decreases and the global dynamics slows down. Such data provide evidence that the approach to the glass transition is accompanied by increasingly long-ranged spatial correlations of the dynamics.

In experiments, direct measurements of χ4(t)�4(�) have been made in colloidal [27] and granular materials [14,15] close to the colloidal and granular glass transitions, and also in foams [28] and gels [29], because dynamics is more easily spatially and temporally resolved in those cases. The results obtained in all these cases are again broadly similar to those shown in Fig. 4, both for the time dependence of χ4(t)�4(�) and its evolution with a change of the relevant variable controlling the dynamics.

Obtaining information on the behavior of χ4(t)�4(�) and G4(r;t)�4(�;�) from experiments on molecular systems is difficult, because it is hard to disentangle the spontaneous fluctuations embodied in χ4(t)�4(�) in Eq. (5) from the experimental noise. Such measurements are, however, crucial because numerical simulations and experiments on colloidal and granular systems can typically only be performed for relaxation times spanning at most 55– 66 decades. On the other hand, in molecular liquids, up to 1414 decades are, in principle, relevant, and extrapolation of simulation data all the way to the experimental glass transition is fraught with difficulty. Indirect estimates of χ4(t)�4(�) from experiments are discussed below.
Real-space measurements and dynamic structure factors


We mentioned above that a growing peak in χ4(t)�4(�) “directly” reveals the growth of a dynamic correlation length scale as the glass transition is approached. This can only be true if the assumptions made in Eq. (3) for the scaling form of G4(r;t)�4(�;�) are correct. Dynamic length scales should, in principle, be obtained by direct measurements of a spatial correlation function.

However, in contrast to χ4(t)�4(�), detailed measurements of G4(r;t)�4(�;�) are technically more challenging as dynamic correlations must be resolved in space over a large range of distances with a very high precision, and so there is much less data to draw on. From the point of view of numerical simulations where many measurements of χ4(t)�4(�) were reported, the main limitation to properly measuring ξ4�4 is the system size. This might seem surprising, as typical numbers extracted for the correlation length scale ξ4�4 are rather modest, but a precise determination of ξ4�4 requires an accurate study of the tail of G4(r;t)�4(�;�) at large r�, which entails considerable numerical effort [30,31].

Such studies are important as they allow the dynamical length scale ξ4(t)�4(�) to be measured directly. Moreover, such studies help infer the behavior of ξ4(t)�4(�) from measurements of χ4(t)�4(�). Published work is consistent with χ4(t)/G4(0,t)�4(�)/�4(0,�) representing the number of particles involved in heterogeneous relaxation. Therefore, truly “direct” measurements indeed confirm that the increase of the peak of χ4(t)�4(�) corresponds, as expected, to a growing dynamic length scale ξ4(t)�4(�) [21,23,26,30,31].

Instead of direct inspection of G4(r;t)�4(�;�), it is often convenient to analyze its Fourier transform,

S4(q;t)=∫ddrexp(iq⋅r)G4(r;t),�4(�;�)=∫��rexp(iq⋅r)�4(�;�),

(6)

which is known as the four-point structure factor of dynamic heterogeneity. In Fourier space, the large domains observed in Fig. 3 affect the low wave vector behavior of S4(q;t)�4(�;�) in the form of a peak that grows when the glass transition is approached. This peak is often fitted with the Ornstein-Zernike functional form that is frequently used in conventional critical phenomena [3].
Experimental estimates of multipoint susceptibilities


Although readily accessible in numerical simulations, the fluctuations that give access to χ4(t)�4(�) are, in general, very small and impossible to measure directly in experiments, except when the range of the dynamic correlation is macroscopic, as in granular materials [14] or in soft glassy materials where it can reach the micrometer and even millimeter range [28,29,32]. To access χ4(t)�4(�) in molecular liquids, one should perform time-resolved dynamic measurements that probe very small volumes, with a linear size of the order of a few nanometers.

Fortunately, simpler alternative procedures exist. The central idea underpinning these solutions is the realization that if it is generally hard to detect noise in an experiment, it is usually simpler to measure the response of a system to an external perturbation. In the linear response regime, both types of measurements can often be related to one another by fluctuation-dissipation theorems [3]. The physical motivation is that while four-point correlations offer a direct probe of the dynamic heterogeneities, other multipoint correlation functions might also give useful information about the microscopic mechanisms leading to these heterogeneities.

For example, one might expect that a local fluctuation of the enthalpy δhx(t=0)�ℎ�(�=0) at position x� and time t=0�=0 triggers or eases the dynamics in its surroundings, leading to a systematic correlation between δhx(t=0)�ℎ�(�=0) and c(x+r;t,0)�(�+�;�,0). A similar effect is expected for a local fluctuation of the density. These physical intuitions suggest the definition of a family of three-point correlation functions that relate thermodynamic fluctuations at one point to dynamical ones at another. Crucially, some of these three-point correlations are both experimentally accessible and give bounds or approximations to the four-point dynamic correlations [33].

Based on this insight, one may obtain a lower bound on χ4(t)�4(�) by using a fluctuation-dissipation relation, which is valid at equilibrium when the energy is conserved by the dynamics [33]:

χ4(t)≥[kBT2/cP]|χT(t)|2,�4(�)≥[���2/��]|��(�)|2,

(7)

where χT(t)��(�) quantifies the response of the average mobility to an infinitesimal change in the temperature T�, and cP�� is the specific heat per particle. The response χT(t)��(�) can be experimentally accessed by measuring the average of a dynamical correlator, ⟨C(t,0)⟩T⟨�(�,0)⟩�, at nearby temperatures, T� and T+δT�+��, in the linear regime δT≪T��≪�:

χT(t)≈[⟨C(t,0)⟩T+δT−⟨C(t,0)⟩T]/δT.��(�)≈[⟨�(�,0)⟩�+��-⟨�(�,0)⟩�]/��.

(8)

The main experimental advantage of Eq. (8) is that spatiotemporal resolution is not needed, contrary to Eq. (5).

Detailed numerical simulations and theoretical arguments [26] strongly suggest that the right-hand side of Eq. (7) actually provides a good estimate of χ4(t)�4(�) in supercooled liquids, and not just a lower bound. Similar estimates exist considering density instead of the temperature in Eq. (8). These are useful when considering colloidal or granular materials where the glass transition is mostly controlled by the packing fraction. The quality of the corresponding lower bound was tested experimentally on granular packings close to the jamming transition [34], and numerically for colloidal hard spheres [30,35].

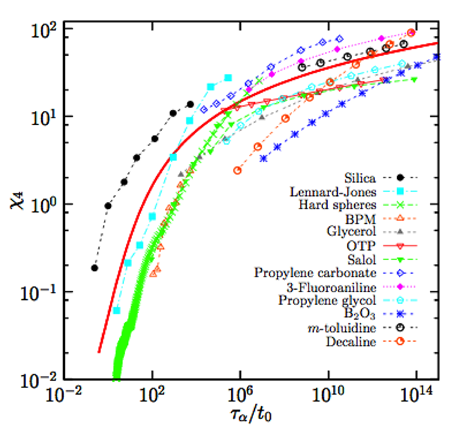
We show in Fig. 5 a compilation of data [36] for the evolution of the peak height of χ4�4, in a representation inspired by the theory of dynamic critical phenomena [3]. These data represent an experimental confirmation that dynamic fluctuations and correlation length scales grow appreciably when molecular liquids approach the glass transition. However, we also learn that typical length scales do not become very large (remaining in the nanometer scale for molecular glass formers) before liquids vitrify in a nonergodic state, and that an “ideal” glass critical point is not readily accessible to experiments.

Figure 5: “Dynamic scaling” relation between the number of dynamically correlated particles, evaluated by the peak height of χ4�4, and relaxation timescale, τα��, for a number of glass-formers [36], determined using the bound provided by Eq. (7). For all systems, dynamic correlations increase when the glass transition is approached. The full line through the data [36] suggests a crossover from algebraic, χ4∼τzα�4∼���, to logarithmic, χ4∼exp(τψα�4∼exp(���), growth of dynamic correlations with increasing τα��.
Theoretical developments


The above results are also relevant as many theories of the glass transition have assumed or predicted that the dynamics slows down because there are increasingly large regions over which particles have to relax in a correlated manner [1]. However, in the absence of experimental signs of growing length scales, these theoretical constructions have remained speculative.

The measurements of the spatial extent of dynamic heterogeneity, in particular χ4(t)�4(�) and G4(r;t)�4(�;�), seem to provide the long-sought evidence that the glass transition must be considered as a form of critical or collective phenomenon involving growing timescales and length scales. This is important for the field of glass transition, even though a conclusive understanding of the relationship between dynamical length scales and relaxation timescales remains the focus of intense research [2].

From a theoretical perspective, we are familiar with the idea, borrowed from equilibrium critical phenomena [3], that when correlation length scales get large, microscopic features of the system become unimportant and “universal” behaviors emerge. Whether realistic glassy systems have length scales that are large enough for such a universal description remains unclear. Although most theoretical approaches are in this spirit, one should perform an equally careful treatment of pre-asymptotic effects, which obviously matter for experiments that are performed far away from (putative) criticality. Therefore, theories of the glass transition are still crude descriptions of reality, despite large research efforts.

Distinct microscopic mechanisms have been proposed that all give rise to growing dynamic correlations similar to the ones revealed by four-point functions. This relative abundance of approaches can be interpreted in two ways. A first view is to consider dynamic heterogeneity as a unifying physical phenomenon that accompanies the formation of glasses, and is central to its theoretical understanding. The second, more pessimistic interpretation is that if any reasonable theory predicts increasingly spatially heterogeneous dynamics, then studying dynamic heterogeneity might not help make substantial theoretical progress. This argument is balanced by the fact that the mere observation of dynamic heterogeneity has forced theorists to work hard on many fronts to understand what sort of microscopic mechanism is able (or not) to provide, for instance, new insights or quantitative predictions for the behavior of multipoint correlation functions, susceptibilities, and dynamic correlation length scales [7].

Several theoretical schemes, such as mode-coupling theory [37], random first-order transition theory [38], dynamic facilitation approach [39], and frustration-limited domain scaling picture [40], have now been developed to the point that they provide useful guides to understand and analyze various aspects of dynamic heterogeneity (see Ref. [2] for a general theoretical review). One hopes that these approaches contain useful seeds for the construction of a “unified” theory of the glassy state. In all of these approaches, dynamic heterogeneity and spatiotemporal fluctuations feature as central concepts.
Perspectives


Although we mostly discussed supercooled liquids near the molecular glass transition, other materials too have played an important role in the development of the concepts and tools described above. Several soft condensed materials, such as colloidal assemblies, have been instrumental in our understanding of the phenomenon of dynamic heterogeneity because they are similar to molecular liquids but with constituents that are so much larger than atoms (in the 50nm50nm– 1μm1�m range) that they can be more easily visualized [13,27]. Driven granular media (sheared or agitated systems) also undergo a “granular” glass transition that is empirically similar to the molecular transition. In that case, grains can be directly tracked using a standard camera [14,15].

In the introduction we alluded to the rigidity transition occurring in athermal disordered granular packings. This “jamming” transition arises in an assembly of rigid particles when the system cannot be compressed anymore, and is thus mainly a geometric transition where thermal fluctuations play no role. For spherical particles of equal sizes, this transition occurs near “random close packing” φrcp≈0.64�rcp≈0.64 [5]. The jamming transition is relevant also for athermal assemblies of soft particles, such as foams and emulsions, which are additional examples of disordered rigid materials [4]. Connections with the physics of glasses are still rather speculative but are currently the focus of an important research effort. Detailed studies of dynamic heterogeneity in packings of soft and hard particles near random close packing started to appear only recently [41–44], and could help elucidate similarities and differences between glasses and granular materials.

One of the most frequently asked questions in studies of dynamical heterogeneity is whether the observed dynamic fluctuations and correlations might have a structural origin: Is there, after all, a “hidden” thermodynamic order parameter that would exhibit spatial fluctuations comparable to the ones revealed by dynamic heterogeneity studies? This question has attracted sustained interest. For example, in very early numerical work on dynamic heterogeneity, immobile regions were discussed in connection with compositional fluctuations in fluid mixtures [45]. However, dynamic heterogeneity would not have emerged as an important concept if a simple, direct connection between structural order and relaxation dynamics had been satisfactorily established in amorphous materials. In that case, research would be dedicated to understanding the development of structural correlations at low temperatures in supercooled liquids, and to developing tools to measure, quantify, and analyze such static features.

Having said that, recent research on isoconfigurational ensembles [46], amorphous order [47], and point-to-set correlations [48] suggests that the structure of disordered materials might be the next topic where new discoveries and concepts emerge. While two-point static correlations are poorly correlated to the evolution of the glassy dynamics, there is plenty of room to invent more complicated correlation functions that would more accurately characterize the local structure of complex disordered media and explain their fascinating physical properties.

#DynamicHeterogeneity#AmorphousMaterials#GlassyState#StructuralRelaxation

#DynamicsInAmorphousMaterials#SpatialHeterogeneity#GlassTransition

#NonEquilibriumSystems#SlowDynamics#AmorphousPhases

Visit:https://condensed-matter.sfconferences.com/ Twitter:https://twitter.com/magnolia2523 Instagram:https://www.instagram.com/magnolia_23baby/ Pinterest:https://in.pinterest.com/condensc/ facebook:https://www.facebook.com/profile.php?id=100092931653336 Linkedin:https://www.linkedin.com/in/mag-nolia-b8157727a/recent-activity/all/